1. INTRODUCCIÓN.
La búsqueda en árboles binarios es un método de búsqueda simple, dinámico y eficiente considerado como uno de los fundamentales en Ciencia de la Computación. De toda la terminología sobre árboles,tan sólo recordar que la propiedad que define un árbol binario es que cada nodo tiene a lo más un hijo a la izquierda y uno a la derecha.Para construir los algoritmos consideraremos que cada nodo contiene un registro con un valor clave a través del cual efectuaremos las búsquedas.En las implementaciones que presentaremos sólo se considerará en cada nodo del árbol un valor del tipo tElemento aunque en un caso general ese tipo estará compuesto por dos:una clave indicando el campo por el cual se realiza la ordenación y una información asociada a dicha clave o visto de otra forma,una información que puede ser compuesta en la cual existe definido un orden.Un árbol binario de búsqueda(ABB) es un árbol binario con la propiedad de que todos los elementos almacenados en el subárbol izquierdo de cualquier nodo x son menores que el elemento almacenado en x,y todos los elementos almacenados en el subárbol derecho de x son mayores que el elemento almacenado en x.
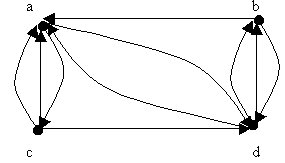
La figura 1 muestra dos ABB construidos en base al mismo conjunto de enteros:
Obsérvese la interesante propiedad de que si se listan los nodos del ABB en inorden nos da la lista de nodos ordenada.Esta propiedad define un método de ordenación similar al Quicksort,con el nodo raíz jugando un papel similar al del elemento de partición del Quicksort aunque con los ABB hay un gasto extra de memoria mayor debido a los punteros.La propiedad de ABB hace que sea muy simple diseñar un procedimiento para realizar la búsqueda. Para determinar si k está presente en el árbol la comparamos con la clave situada en la raíz, r.Si coinciden la búsqueda finaliza con éxito, si k<r es evidente quek,de estar presente,ha de ser un descendiente del hijo izquierdo de la raíz,y si es mayor será un descendiente del hijo derecho.La función puede ser codificada fácilmente de la siguiente forma:
#define ABB_VACIO NULL
#define TRUE 1
#define FALSE 0
typedef int tEtiqueta /*Algun tipo adecuado*/
typedef struct tipoceldaABB{
struct tipoceldaABB *hizqda,*hdrcha;
tEtiqueta etiqueta;
}*nodoABB;
typedef nodoABB ABB;
ABB Crear(tEtiqueta et)
{
ABB raiz;
raiz = (ABB)malloc(sizeof(struct tceldaABB));
if (raiz == NULL)
error("Memoria Insuficiente.");
raiz->hizda = NODO_NULO;
raiz->hdcha = NODO_NULO;
raiz->etiqueta = et;
return(raiz);
}
int Pertenece(tElemento x,ABB t)
{
if(!t)
return FALSE
else if(t->etiqueta==x)
return TRUE;
else if(t->etiqueta>x)
return pertenece(x,t->hizqda);
else return pertenece(x,t->hdrcha);
}
Es conveniente hacer notar la diferencia entre este procedimiento y el de búsqueda binaria.En éste podría pensarse en que se usa un árbol binario para describir la secuencia de comparaciones hecha por una función de búsqueda sobre el vector.En cambio en los ABB se construye una estructura de datos con registros conectados por punteros y se usa esta estructura para la búsqueda.El procedimiento de construcción de un ABB puede basarse en un procedimiento de inserción que vaya añadiendo elementos al árbol. Tal procedimiento comenzaría mirando si el árbol es vacío y de ser así se crearía un nuevo nodo para el elemento insertado devolviendo como árbol resultado un puntero a ese nodo.Si el árbol no está vacio se busca el elemento a insertar como lo hace el procedimiento pertenece sólo que al encontrar un puntero NULL durante la búsqueda,se reemplaza por un puntero a un nodo nuevo que contenga el elemento a insertar.El código podría ser el siguiente:
void Inserta(tElemento x,ABB *t)
{
if(!(*t)){
*t=(nodoABB)malloc(sizeof(struct tipoceldaABB));
if(!(*t)){
error("Memoria Insuficiente.");
}
(*t)->etiqueta=x;
(*t)->hizqda=NULL;
(*t)->hdrcha=NULL;
} else if(x<(*t)->etiqueta)
inserta(x,&((*t)->hizqda));
else
inserta(x,&((*t)->hdrcha));
}
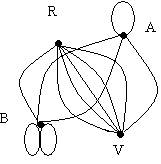
Por ejemplo supongamos que queremos construir un ABB a partir del conjunto de enteros {10,5,14,7,12} aplicando reiteradamente el proceso de inserción.El resultado es el que muestra la figura 2.
2. ANÁLISIS DE LA EFICIENCIA DE LAS OPERACIONES.
Puede probarse que una búsqueda o una inserción en un ABB requiere O(log2n) operaciones en el caso medio,en un árbol construido a partir de n claves aleatorias, y en el peor caso una búsqueda en un ABB con n claves puede implicar revisar las n claves,o sea,es O(n).Es fácil ver que si un árbol binario con n nodos está completo (todos los nodos no hojas tienen dos hijos) y así ningún camino tendrá más de 1+log2n nodos.Por otro lado,las operaciones pertenece e insertatoman una cantidad de tiempo constante en un nodo.Por tanto,en estos árboles, el camino que forman desde la raíz,la secuencia de nodos que determinan la búsqueda o la inserción, es de longitud O(log2n),y el tiempo total consumido para seguir el camino es también O(log2n).
Sin embargo,al insertar n elementos en un orden aleatorio no es seguro que se sitúen en forma de árbol binario completo.Por ejemplo,si sucede que el primer elemento(de n situados en orden) insertado es el más pequeño el árbol resultante será una cadena de n nodos donde cada nodo,excepto el más bajo en el árbol,tendrá un hijo derecho pero no un hijo izquierdo.En este caso,es fácil demostrar que como llevai pasos insertar el i-ésimo elemento dicho proceso de n inserciones necesita
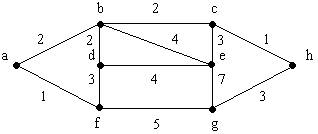
pasos o equivalentemente O(n) pasos por operación.Es necesario pues determinar si el ABB promedio con n nodos se acerca en estructura al árbol completo o a la cadena,es decir,si el tiempo medio por operación es O(log2n),O(n) o una cantidad intermedia.Como es difícil saber la verdadera frecuencia de inserciones sólo se puede analizar la longitud del camino promedio de árboles "aleatorios" adoptando algunas suposiciones como que los árboles se forman sólo a partir de inserciones y que todas las magnitudes de los n elementos insertados tienen igual probabilidad.Con esas suposiciones se puede calcular P(n),el número promedio de nodos del camino que va de la raíz hacia algún nodo(no necesariamente una hoja).Se supone que el árbol se formó con la inserción aleatoria de n nodos en un árbol que se encontraba inicialmente vacío,es evidente que P(0)=0 y P(1)=1.Supongamos que tenemos una lista de n>=2 elementos para insertar en un árbol vacío,el primer elemento de la lista,x,es igual de probable que sea el primero,el segundo o el n-ésimo en la lista ordenada.Consideremos que i elementos de la lista son menores que x de modo que n-i-1 son mayores. Al construir el árbol,x aparecerá en la raíz,los i elementos más pequeños serán descendientes izquierdos de la raíz y los restantes n-i-1 serán descendientes derechos.Esquemáticamente quedaría como muestra la figura 3.
Al tener tanto en un lado como en otro todos los elementos igual probabilidad se espera que los subárboles izqdo y drcho de la raíz tengan longitudes de camino medias P(i) y P(n-i-1) respectivamente.Como es posible acceder a esos elementos desde la raíz del árbol completo es necesario agregar 1 al número de nodos de cada camino de forma que para todo i entre 0 y n-1,P(n) puede calcularse obteniendo el promedio de la suma:
El primer término es la longitud del camino promedio en el subárbol izquierdo ponderando su tamaño.El segundo término es la cantidad análoga del subárbol derecho y el término 1/n representa la contribución de la raíz.Al promediar la suma anterior para todo i entre 1 y n se obtiene la recurrencia:
y con unas transformaciones simples podemos ponerla en la forma:
y el resto es demostrar por inducción sobre n que P(n)<=1+4log2n.
En consecuencia el tiempo promedio para seguir un camino de la raíz a un nodo aleatorio de un ABB construido mediante inserciones aleatorias es O(log2n).Un análisis más detallado demuestra que la constante 4 es en realidad una constante cercana a 1.4.
De lo anterior podemos concluir que la prueba de pertenencia de una clave aleatoria lleva un tiempo O(log2n).Un análisis similar muestra que si se incluyen en la longitud del camino promedio sólo aquellos nodos que carecen de ambos hijos o solo aquellos que no tienen hijo izqdo o drcho también la longitud es O(log2n).
Terminaremos este apartado con algunos comentarios sobre los borrados en los ABB.Es evidente que si el elemento a borrar está en una hoja bastaría eliminarla,pero si el elemento está en un nodo interior,eliminándolo,podríamos desconectar el árbol.Para evitar que esto suceda se sigue el siguiente procedimiento:si el nodo a borrar u tiene sólo un hijo se sustituye u por ese hijo y el ABB quedar&aacue; construido.Si u tiene dos hijos,se encuentra el menor elemento de los descendientes del hijo derecho(o el mayor de los descendientes del hijo izquierdo) y se coloca en lugar de u,de forma que se continúe manteniendo la propiedad de ABB.
V. G es llamado un multigrafo dirigido y geométricamente puede representarse como un conjunto de vértices V y un conjunto de flechas E entre los vértices, donde no existe restricción en el numero de flechas de un vértice a otro.
, si existen bisecciones 
,
en un digrafo D se dice que es una cadena si k = 1 o k > 1y las aristas 
son distintas dos a dos.
D es Hamiltoniano.
entonces D es Hamiltoniano.
Para las
, puesto que hay 10 semillas de flores rojas de un total de 15. Escrito con notación de probabilidad tenemos: 
, puesto que todavía hay 5 semillas blancas en un total de 14 restantes.
.
es la probabilidad de una ocurrencia en las siete que son posibles en A; es decir, calcular la probabilidad condicional de B dado A es como calcular la probabilidad de B con relación al conjunto A, como si éste fuera un nuevo espacio muestra S* = A.
[3.3]
se llama también número combinatorio. Se representa por 
y se lee "m sobre n".
